Pengertian Integral: Kebalikan dari proses diferensiasi fungsi. – Pernah nggak sih kamu merasa seperti Indiana Jones yang sedang memecahkan teka-teki kuno, tapi teka-tekinya berupa angka dan simbol aneh? Halo, para petualang matematika! Kali ini, kita akan menyelami dunia “Integral,” sebuah konsep yang mungkin terdengar menakutkan, tapi sebenarnya adalah kunci untuk memahami banyak hal di sekitar kita. Siap berpetualang?
Bayangkan kamu sedang mengisi air ke dalam kolam renang. Integral membantumu menghitung berapa banyak air yang dibutuhkan, bahkan jika keran airnya nggak konsisten mengalirkan air. Atau, coba pikirkan tentang kecepatan mobilmu yang berubah-ubah. Integral bisa membantumu menghitung jarak yang kamu tempuh, walau jarum speedometer nggak pernah diam. Keren, kan?
Intinya, integral adalah kebalikan dari turunan. Kalau turunan membantumu melihat perubahan suatu fungsi, integral membantumu mengumpulkan perubahan-perubahan itu kembali menjadi bentuk aslinya. Ia adalah alat ampuh yang digunakan di berbagai bidang, mulai dari fisika, ekonomi, sampai ilmu komputer. Jadi, jangan anggap remeh si integral ini ya!
Memahami integral bukan cuma soal mengerjakan soal ujian. Lebih dari itu, integral membuka pintu ke pemahaman yang lebih dalam tentang dunia di sekeliling kita. Ia melatih logika, meningkatkan kemampuan problem-solving, dan memberikan perspektif baru dalam melihat perubahan dan akumulasi. Yuk, kita mulai petualangan integral ini bersama-sama!
Oke siap! Ini dia artikel tentang ‘Integral’ yang lengkap, mendalam, dan ditulis dengan gaya storytelling yang asyik, seolah-olah kita lagi ngobrol santai sambil ngopi. Dijamin, setelah baca ini, kamu bakal paham Integral luar dalam!
Memahami Integral: Lebih dari Sekadar Rumus, Ini Kisah di Baliknya!
Integral: Menjelajahi Luasnya Dunia dengan Matematika
Pernahkah kamu membayangkan bagaimana caranya menghitung luas area yang bentuknya aneh, nggak beraturan, kayak daun atau pulau? Atau mungkin, bagaimana kita bisa tahu berapa total jarak yang ditempuh mobil kalau kecepatannya berubah-ubah setiap detik? Nah, di sinilah Integral hadir sebagai pahlawan! Integral itu kayak detektif matematika yang bisa mengungkap misteri-misteri perhitungan yang rumit. Secara sederhana, Integral adalah kebalikan dari turunan (diferensial). Kalau turunan itu memecah sesuatu jadi bagian-bagian kecil, Integral justru menyatukan bagian-bagian kecil itu untuk mencari totalnya. Jadi, bayangkan kamu punya puzzle yang sudah diacak-acak. Integral itu kayak tangan ajaib yang menyusun kembali puzzle itu jadi gambar yang utuh dan indah.
Lebih dari sekadar rumus dan simbol-simbol aneh, Integral itu sebenarnya adalah alat yang sangat powerful untuk memodelkan dan memahami dunia di sekitar kita. Dari menghitung volume benda-benda tiga dimensi, memprediksi pertumbuhan populasi, sampai menganalisis sinyal listrik, Integral punya peran penting di berbagai bidang. Jadi, jangan anggap Integral itu cuma momok di pelajaran matematika ya! Integral itu sahabat yang siap membantu kita memecahkan masalah-masalah kompleks dengan cara yang elegan dan efisien.
Definisi Integral Menurut Para Ahli: Sebuah Simfoni Perspektif
Kayak lagi dengerin musik, Integral itu punya banyak interpretasi dari berbagai ahli. Masing-masing punya sudut pandang yang unik, tapi semuanya sepakat bahwa Integral itu penting banget!
- Isaac Newton (1687): “Integral adalah metode untuk menemukan kuantitas yang fluksionya (turunannya) diketahui.” (Newton melihat Integral sebagai kebalikan dari proses diferensiasi, fokus pada mencari fungsi asal dari turunannya).
- Gottfried Wilhelm Leibniz (1675): “Integral adalah penjumlahan tak hingga dari elemen-elemen infinitesimal.” (Leibniz menekankan ide menjumlahkan bagian-bagian yang sangat kecil untuk mendapatkan totalnya, konsep yang sangat visual dan intuitif).
- Bernhard Riemann (1854): “Integral adalah limit dari jumlah Riemann, yang merupakan pendekatan luas area di bawah kurva dengan menggunakan persegi panjang.” (Riemann memberikan definisi yang lebih formal dan matematis, mendefinisikan Integral sebagai limit dari proses aproksimasi).
- Henri Lebesgue (1902): “Integral adalah generalisasi dari integral Riemann yang memungkinkan integrasi fungsi yang lebih luas, termasuk fungsi yang tidak kontinu.” (Lebesgue memperluas konsep Integral agar bisa diterapkan pada fungsi-fungsi yang lebih kompleks dan “bermasalah”).
Jadi, dari Newton yang melihat Integral sebagai kebalikan turunan, Leibniz yang menekankan penjumlahan elemen kecil, Riemann dengan aproksimasi luas area, sampai Lebesgue yang memperluas cakupan fungsi yang bisa diintegralkan, kita bisa lihat bahwa Integral itu konsep yang kaya dan terus berkembang. Masing-masing definisi memberikan insight yang berharga dan saling melengkapi untuk memahami Integral secara utuh.
Sejarah Integral: Dari Zaman Kuno Hingga Era Digital
Kisah Integral itu panjang dan berliku, dimulai jauh sebelum kalkulus modern ditemukan. Ide dasar Integral, yaitu menghitung luas dan volume, sudah ada sejak zaman Mesir Kuno dan Yunani Kuno. Mereka menggunakan metode aproksimasi yang sederhana, seperti membagi area menjadi bentuk-bentuk yang lebih kecil dan mudah dihitung.
Archimedes, seorang matematikawan Yunani yang hidup sekitar abad ke-3 SM, dianggap sebagai salah satu pelopor Integral. Dia berhasil menghitung luas lingkaran dan volume bola dengan metode yang sangat cerdik, yaitu dengan membagi bentuk-bentuk tersebut menjadi bagian-bagian yang tak terhingga kecilnya. Bayangin, ribuan tahun lalu, tanpa kalkulus modern, Archimedes sudah bisa melakukan hal itu! Keren banget, kan? Memahami organisasi kehidupan dimulai dengan mempelajari sel, karena Struktur Sel Peranannya dalam menjalankan fungsi vital organisme
Namun, perkembangan Integral yang sesungguhnya baru terjadi pada abad ke-17, berkat kerja keras Isaac Newton dan Gottfried Wilhelm Leibniz. Mereka secara independen mengembangkan kalkulus, yang mencakup konsep turunan dan Integral. Newton menggunakan kalkulus untuk menjelaskan hukum gravitasi dan gerak planet, sementara Leibniz mengembangkan notasi matematika yang kita gunakan sampai sekarang. Jadi, bisa dibilang, Newton dan Leibniz adalah “bapak” dan “ibu” Integral modern.
Sejak saat itu, Integral terus berkembang dan diaplikasikan di berbagai bidang, mulai dari fisika, teknik, ekonomi, sampai ilmu komputer. Di era digital ini, Integral digunakan untuk memodelkan dan menganalisis data yang kompleks, membuat prediksi, dan mengoptimalkan berbagai proses. Jadi, Integral itu bukan cuma sejarah, tapi juga masa depan! Dalam ekosistem yang kompleks, kita menemukan bahwa Mutualisme Kerjasama Saling adalah fondasi hubungan yang berkelanjutan
Mengupas Karakteristik Integral: Apa yang Membuatnya Istimewa?
Integral: Jembatan Antara Bagian Kecil dan Keseluruhan
Salah satu hal yang paling menarik dari Integral adalah kemampuannya untuk menghubungkan bagian-bagian kecil dengan keseluruhan. Bayangkan kamu punya peta yang sangat detail, tapi kamu cuma melihat sebagian kecil dari peta itu. Integral itu kayak alat yang bisa membantu kamu menyatukan semua bagian kecil peta itu, sehingga kamu bisa melihat gambaran utuh dari seluruh wilayah.
- Kebalikan dari Turunan: Integral adalah operasi matematika yang “membatalkan” efek turunan. Kalau turunan itu mencari laju perubahan suatu fungsi, Integral mencari fungsi asalnya.
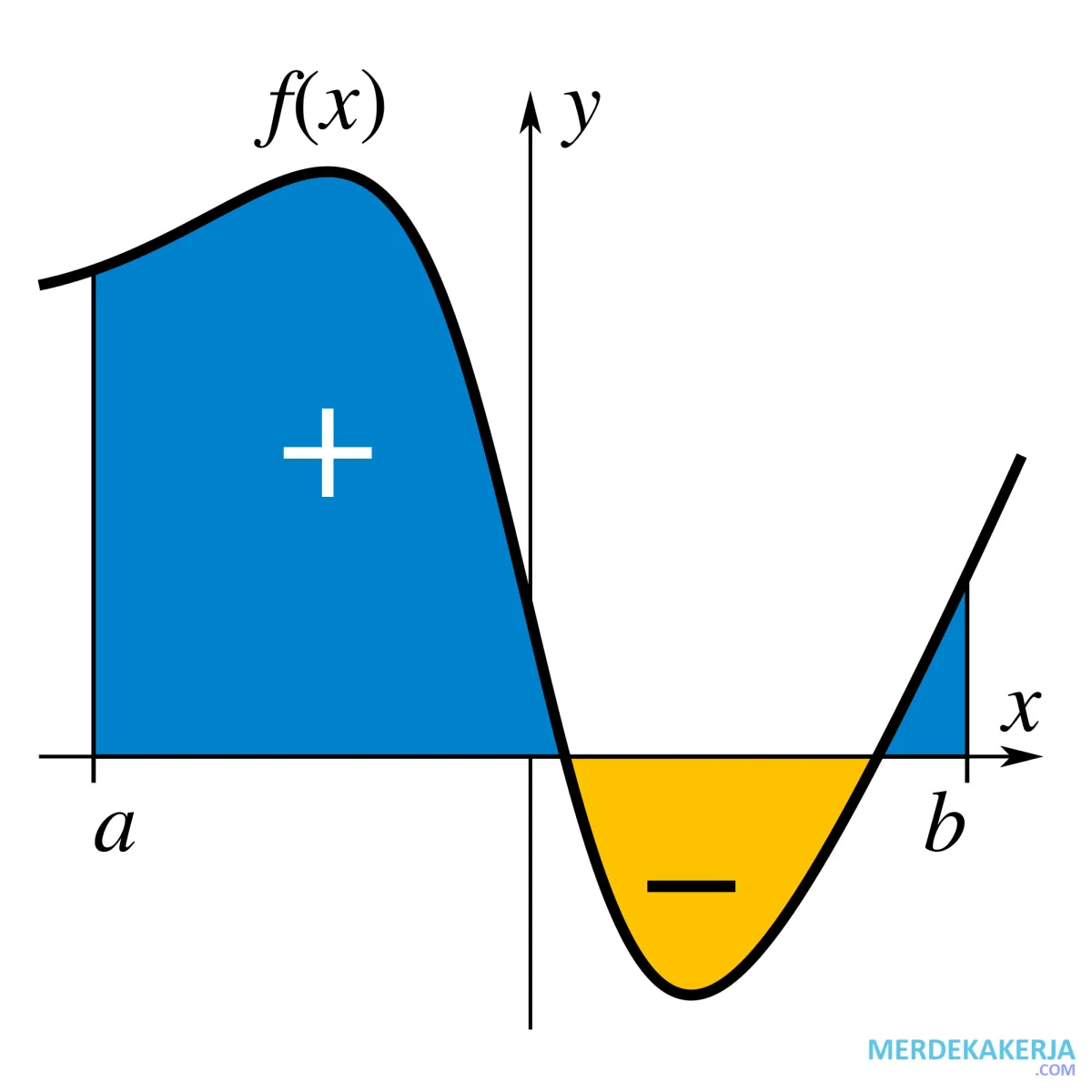
- Menghitung Luas Area di Bawah Kurva: Ini adalah salah satu aplikasi Integral yang paling populer dan mudah dipahami. Integral bisa menghitung luas area yang dibatasi oleh kurva dan sumbu-x.
- Menghitung Volume Benda Putar: Integral juga bisa digunakan untuk menghitung volume benda yang dihasilkan dari memutar suatu kurva di sekitar sumbu.
- Menyelesaikan Persamaan Diferensial: Persamaan diferensial adalah persamaan yang melibatkan turunan. Integral bisa digunakan untuk mencari solusi dari persamaan diferensial, yang sering muncul dalam masalah fisika dan teknik.
- Aplikasi Luas di Berbagai Bidang: Seperti yang sudah disebutkan sebelumnya, Integral punya aplikasi yang sangat luas di berbagai bidang, mulai dari fisika, teknik, ekonomi, sampai ilmu komputer.
Integral: Lebih dari Sekadar Luas, Ini tentang Akumulasi dan Perubahan
Meskipun sering dikaitkan dengan menghitung luas area, Integral sebenarnya lebih dari itu. Integral adalah tentang akumulasi dan perubahan. Integral bisa digunakan untuk menghitung total perubahan suatu kuantitas seiring waktu, seperti total jarak yang ditempuh mobil, total energi yang dikonsumsi, atau total populasi yang bertambah.
Jadi, bayangkan kamu punya keran yang meneteskan air ke dalam ember. Integral itu kayak alat yang bisa menghitung berapa banyak air yang sudah terkumpul di dalam ember seiring waktu. Atau bayangkan kamu punya grafik yang menunjukkan pertumbuhan populasi suatu spesies. Integral itu kayak alat yang bisa menghitung total pertambahan populasi selama periode waktu tertentu.
Jenis-Jenis Integral: Dari yang Sederhana Hingga yang Rumit
Integral Tak Tentu (Indefinite Integral): Mencari Keluarga Fungsi
Integral tak tentu adalah jenis Integral yang paling dasar. Hasil dari Integral tak tentu adalah sebuah keluarga fungsi, bukan sebuah nilai tunggal. Kenapa bisa begitu? Karena Integral tak tentu selalu memiliki konstanta integrasi (+C). Konstanta ini menunjukkan bahwa ada banyak fungsi yang memiliki turunan yang sama.
- Integral Fungsi Aljabar: Integral dari fungsi-fungsi seperti x², 3x + 5, atau √x. Rumus dasar Integral fungsi aljabar adalah ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, dengan n ≠ -1.
- Integral Fungsi Trigonometri: Integral dari fungsi-fungsi seperti sin(x), cos(x), tan(x), dan sebagainya. Contohnya, ∫sin(x) dx = -cos(x) + C dan ∫cos(x) dx = sin(x) + C.
- Integral Fungsi Eksponensial dan Logaritma: Integral dari fungsi-fungsi seperti eˣ dan ln(x). Contohnya, ∫eˣ dx = eˣ + C dan ∫(1/x) dx = ln|x| + C.
Integral Tentu (Definite Integral): Menghitung Luas yang Pasti
Integral tentu adalah jenis Integral yang memiliki batas atas dan batas bawah. Hasil dari Integral tentu adalah sebuah nilai tunggal, yang merepresentasikan luas area di bawah kurva antara batas atas dan batas bawah tersebut. Integral tentu tidak memiliki konstanta integrasi (+C).
Integral Lipat (Multiple Integral): Menjelajahi Dimensi yang Lebih Tinggi
Integral lipat adalah generalisasi dari Integral biasa ke fungsi dengan lebih dari satu variabel. Integral lipat digunakan untuk menghitung volume benda tiga dimensi, massa benda dengan densitas yang bervariasi, dan sebagainya. Ada beberapa jenis Integral lipat, seperti Integral ganda (double integral) dan Integral triple (triple integral).
Fungsi dan Manfaat Integral: Mengapa Integral Penting dalam Hidup Kita?
Integral: Alat Bantu yang Tak Ternilai di Berbagai Bidang
Integral bukan cuma sekadar rumus yang bikin pusing kepala. Integral adalah alat bantu yang sangat powerful dan tak ternilai di berbagai bidang. Dari fisika sampai ekonomi, Integral punya peran penting dalam memecahkan masalah-masalah kompleks dan memodelkan dunia di sekitar kita.
- Fisika: Menghitung kerja yang dilakukan oleh gaya, menghitung pusat massa benda, menganalisis gerak partikel.
- Teknik: Menghitung tegangan dan regangan pada struktur, merancang sirkuit listrik, menganalisis aliran fluida.
- Ekonomi: Menghitung surplus konsumen dan produsen, memprediksi pertumbuhan ekonomi, menganalisis investasi.
Manfaat Praktis Integral: Dari Roket Hingga Keuangan
Manfaat Integral itu nggak cuma teoritis, tapi juga sangat praktis dan bisa kita rasakan dalam kehidupan sehari-hari. Bayangin, tanpa Integral, kita nggak akan bisa menerbangkan roket ke luar angkasa, merancang jembatan yang kokoh, atau membuat prediksi keuangan yang akurat.
Integral digunakan untuk menghitung lintasan roket, sehingga roket bisa mencapai target dengan tepat. Integral digunakan untuk menghitung kekuatan material yang digunakan untuk membangun jembatan, sehingga jembatan bisa menahan beban yang berat. Integral digunakan untuk menganalisis data keuangan dan membuat prediksi tentang pasar saham, sehingga investor bisa membuat keputusan yang cerdas.
Contoh dan Implementasi Integral: Biar Makin Paham!
Integral dalam Aksi: Contoh-Contoh Praktis
Biar kamu makin paham tentang Integral, yuk kita lihat beberapa contoh praktisnya!
- Menghitung Jarak Tempuh Mobil: Misalkan kamu punya grafik yang menunjukkan kecepatan mobil seiring waktu. Integral dari grafik kecepatan ini akan memberikan total jarak yang ditempuh mobil.
- Menghitung Volume Kolam Renang: Misalkan kamu punya kolam renang yang bentuknya nggak beraturan. Integral bisa digunakan untuk menghitung volume kolam renang dengan membagi kolam renang menjadi lapisan-lapisan tipis dan menjumlahkan volume setiap lapisan.
- Menghitung Surplus Konsumen: Dalam ekonomi, surplus konsumen adalah selisih antara harga yang bersedia dibayar konsumen dengan harga pasar. Integral bisa digunakan untuk menghitung surplus konsumen dengan menghitung area di bawah kurva permintaan dan di atas harga pasar.
Studi Kasus: Integral dalam Desain Jembatan
Jembatan Golden Gate: Keajaiban Teknik Berkat Integral
Jembatan Golden Gate adalah salah satu jembatan paling ikonik di dunia. Desain jembatan ini melibatkan perhitungan yang sangat kompleks, termasuk perhitungan tegangan dan regangan pada kabel dan menara jembatan. Integral memainkan peran penting dalam perhitungan ini. Para insinyur menggunakan Integral untuk memodelkan gaya yang bekerja pada jembatan dan memastikan bahwa jembatan bisa menahan beban yang berat dan angin kencang. Tanpa Integral, jembatan Golden Gate mungkin nggak akan pernah bisa dibangun!
Tips dan Panduan Praktis Belajar Integral
Belajar Integral memang butuh kesabaran dan latihan. Tapi jangan khawatir, ada beberapa tips dan panduan yang bisa membantu kamu!
- Pelajari konsep dasar Integral dengan baik.
- Latihan soal secara teratur.
- Gunakan sumber belajar yang berkualitas, seperti buku teks, video tutorial, atau website interaktif.
- Jangan takut bertanya jika ada yang nggak kamu mengerti.
Gimana? Sudah lebih paham tentang Integral kan? Ingat, Integral itu bukan momok, tapi sahabat yang siap membantu kita memecahkan masalah-masalah kompleks. Jadi, jangan menyerah dan teruslah belajar! Semangat!
Kesimpulan
Jadi, gimana nih obrolan kita tentang integral? Seru kan? Kita udah sama-sama menyelami apa itu integral, bukan cuma sekadar rumus atau simbol-simbol aneh di buku pelajaran. Kita udah lihat kalau integral itu sebenarnya adalah cara keren buat ngitung luas area yang bentuknya nggak beraturan, atau buat nemuin fungsi aslinya kalau kita cuma tahu perubahan kecepatannya aja. Intinya, integral itu alat yang super powerful buat mecahin masalah di dunia nyata, dari ngedesain jembatan yang kokoh sampai memprediksi pertumbuhan populasi. Keren, kan?
Nah, sekarang kamu udah punya gambaran yang lebih jelas tentang integral. Jangan berhenti di sini ya! Matematika itu kayak petualangan tanpa akhir. Semakin kamu dalami, semakin banyak hal menakjubkan yang bisa kamu temukan. Jadi, teruslah penasaran, teruslah belajar, dan jangan takut buat nyoba soal-soal yang menantang. Siapa tahu, dengan memahami integral, kamu bisa nemuin solusi buat masalah-masalah besar di masa depan! Ingat, matematika itu bukan cuma angka dan rumus, tapi juga mindset yang bisa ngebantu kita berpikir lebih logis dan kreatif. Selamat berpetualang di dunia integral! Untuk memahami bagaimana tubuh kita bekerja secara harmonis, mari kita selami Sistem Koordinasi Tubuh yang mengatur segalanya
Oke, siap! Mari kita buat FAQ tentang integral dengan gaya storytelling yang asik dan mudah dimengerti. Anggap aja kita lagi ngobrol santai sambil ngopi, ya!
FAQ tentang Integral
Integral itu sebenarnya buat apa sih? Kok kayaknya nyeremin banget?
Nah, ini pertanyaan yang sering banget muncul! Jujur, dulu aku juga mikir gitu. Integral itu kayak monster matematika yang bikin pusing. Tapi, bayangin gini deh, kamu punya kurva yang bentuknya nggak karuan. Terus kamu pengen tahu luas area di bawah kurva itu? Nah, integral ini jagoannya! Dia bisa menghitung luas, volume, bahkan total perubahan dari sesuatu yang terus menerus berubah. Jadi, jangan takut! Integral itu sebenarnya alat yang super powerful buat memecahkan masalah di dunia nyata, mulai dari fisika, ekonomi, sampai teknik.
Bedanya integral tak tentu sama integral tentu itu apa ya? Kok bikin bingung?
Oke, ini seringkali jadi batu sandungan. Jadi gini, integral tak tentu itu kayak lagi nyari “keluarga” fungsi. Hasilnya berupa fungsi baru ditambah konstanta (si “+ C” yang misterius itu). Kenapa ada + C? Karena turunan dari konstanta itu nol, jadi kita nggak tahu aslinya berapa. Nah, kalau integral tentu, kita punya batas atas dan batas bawah. Kita hitung integralnya, lalu masukkin batas-batas itu. Hasilnya berupa angka konkret, bukan lagi fungsi. Jadi, kalau integral tak tentu itu nyari fungsi, integral tentu itu nyari nilai pasti.
Gimana caranya biar jago ngerjain soal integral? Ada tips dan triknya nggak?
Rahasia jago integral? Latihan, latihan, dan latihan! Serius deh. Pertama, kuasai dulu konsep dasar turunan, karena integral itu kebalikannya. Kedua, hafalkan rumus-rumus dasar integral. Ketiga, jangan takut mencoba berbagai teknik integrasi (substitusi, parsial, dll.). Kalau mentok, jangan malu bertanya! Manfaatkan internet, buku, atau teman yang lebih paham. Dan yang paling penting, jangan menyerah! Anggap aja integral itu puzzle yang menantang, bukan momok yang menakutkan. Semangat!
Semoga FAQ ini membantu dan bikin kamu makin semangat belajar integral, ya! 😉



